

Let us check the examples of a few of the equations which represent a function, and a few equations which do not represent functions.Įquations representing functions: y = x, y = x 2, y = 3, y = |x|, y = Sinx, y = x 3, y = \(3\sqrt x\),Įquations which do not represent functions: x = y 2, x 2 + y 2 = 9, x = 4, y = \(\sqrt x\) In the above graph, the three graphs towards the left have the vertical lines cutting it at only one point, and hence they represent a function, and the three graphs towards the right do not represent the function as the vertical line cuts the graph at two points. For a function, the vertical line needs to cut the curve at only one point. If the line is cutting the curve more than once, then it does not represent the graph of a function. In each of the graphs, we can conclude by a quick observation if the vertical line is cutting the curve at one point or more than one point. If a vertical line intersects the graph of the relation at only one point, then it is a function, and if it intersects at more than one point then the graph does not represent a function.Ī graph of a vertical line helps to easily identify if the given equation y = f(x) represents a function or not. Thus each domain has more than one codomain value and it contradicts the basic definition of a function, and the curve y = f(x) does not represent a function.Ī function is expected to have a unique range for each of its domains, and if the input has more than one output, then it is not considered a function: this can be identified using the vertical line test. at two points such as (x, y 1), (x, y 2), then it is having different y values for the same x-value. And if the vertical line x = a is cutting the graph y = f(x) at more than one point, ie.
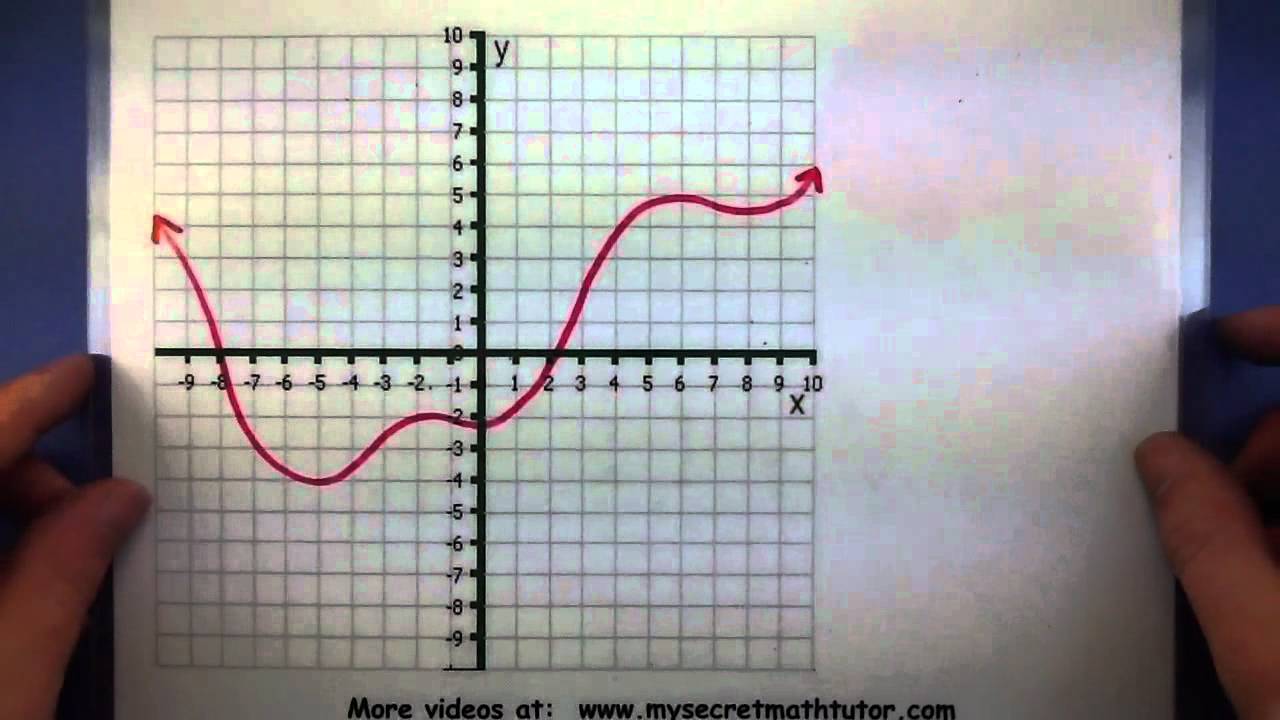
The vertical line x = a, if it cuts the curve y = f(x) at only one point (a, f(a)), then such a curve y = f(x) represents a function.Ī vertical line is supposed to cut the curve at only one point, for the curve to represent a function. The vertical line test satisfies the definition of a function: for every domain x value, there is only one range y value for the function. The vertical line test is helpful in knowing if a relation is a function or not. The vertical line is drawn parallel to the y-axis, if it cuts the curve at one distinct point then it has one y-value for the given x value and it follows the basic definition of a function. The vertical line in a coordinate system represents a set of infinite points having the same x coordinate values and different y coordinate values for each of its points. A vertical line test helps to find if the graph is a function or not.


 0 kommentar(er)
0 kommentar(er)
